现金九游体育app平台方程1689蕴含方程2的阐发-Ninegame-九游体育(中国)官方网站|jiuyou.com

新智元报说念

剪辑：桃子 好困

【新智元导读】AI已统统融入数学家的使命流中。陶哲轩刚刚晓喻，最新方程表面技俩已完成99.9963%，众包之力外加AI援助取得了紧要获利。他以为，剩余轻便700个让东说念主类头疼的难题，AI大要更有后劲。

AI，已成为菲尔兹奖得主最轻车熟路的用具。

轻便三周前，陶哲轩建议了一个合作技俩——

调处专科和业尾数学家、自动定理阐发器、AI用具，以及阐发援助话语Lean，来神色与4694条幺半群（magmas）方程定理定理相干的蕴含图。

这些定理最多不错使用，四次幺半群运算来抒发。

也等于说，需要细目4694条定理之间可能存在4694 * (4694 - 1) = 22028942蕴含的关系真伪。

地址：https://github.com/teorth/equational_theories/blob/main/data/equations.txt

这一技俩在9月25日发布本日便启动了，如今，也曾紧锣密饱读进行了19天。

刚刚，陶哲轩公布了项贪图最新进展：

从已管理原始蕴含关系角度来看，规章现时，技俩程度已完成99.9963%。 在需要管理的22028942个蕴含关系中，8178279个被阐发为真，13854531个被阐发为假，独一826个仍未管理。

而且，技俩每一天的进展，他王人纪录到了个东说念主日记中。

一说念望望，陶哲轩如何通过「众包形状」，探索数学新范围。

方程表面技俩，程度99.99%

在麇聚合，有249个蕴含关系谈论为假，何况很快就阐发了是假的。

出于编译弃世的考量，他们并莫得在Lean中纪录每一个阐发，只在其中阐发了一个较小的592790个蕴含关系网络，然后通过传递性推导出更庸俗的蕴含关系网络。

举例，运用如果方程X蕴含方程Y，方程Y蕴含方程Z，那么方程X蕴含方程Z的事实。

他们还很快运用蕴含图对偶对称性，对其进一步简化。

经过技俩志愿者的不懈力图，陶哲轩称现时有了许多出色的可视化用具（尚未完成的），来检验蕴含图的各个部分。

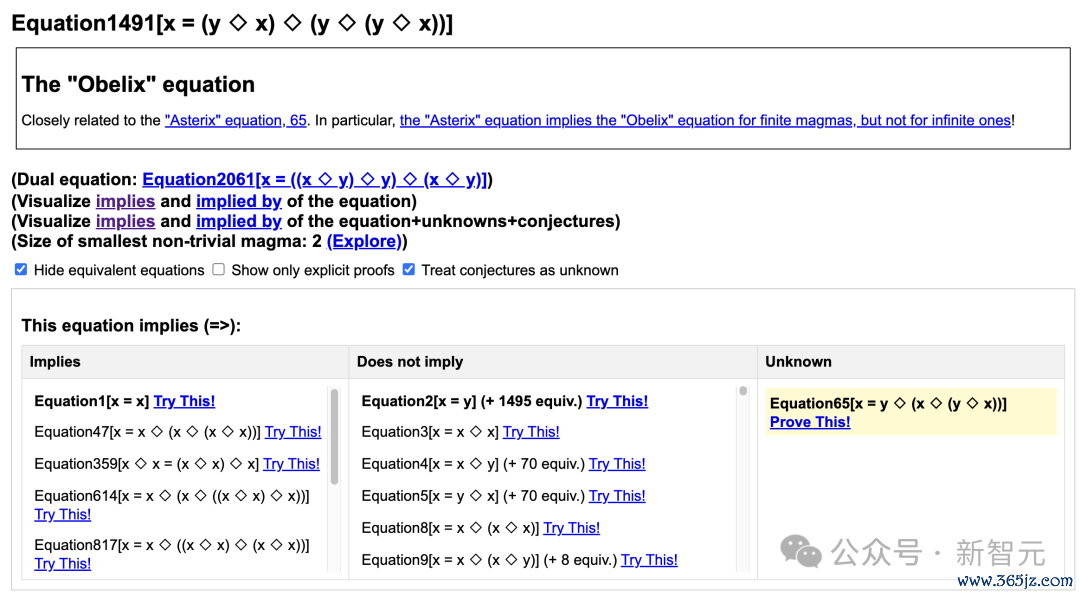
比如，如下这张图神色了方程1491：x = (y ◇ x) ◇ (y ◇ (y ◇ x ))的通盘弃世。

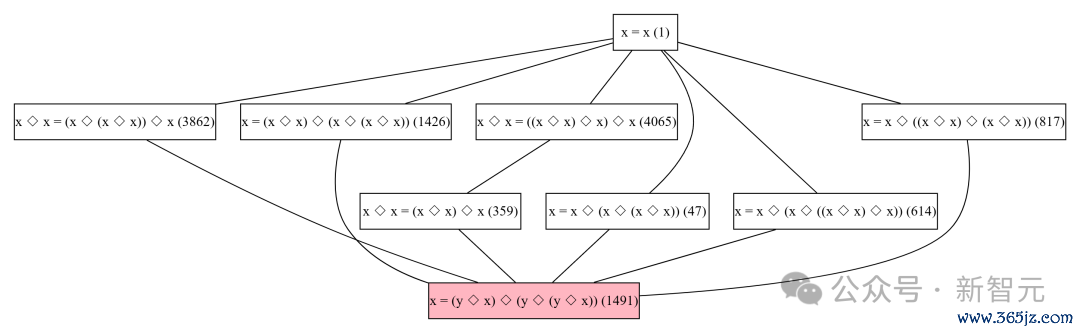
陶哲轩将其称之为「Obelix law」。它还有一个伙伴Asterix law，即方程65：x = y ◇ (x ◇ (y ◇ x ))。

如下是，他们正在磋商的通盘方程定理的表格，以及它们蕴含/被蕴含定理数目。

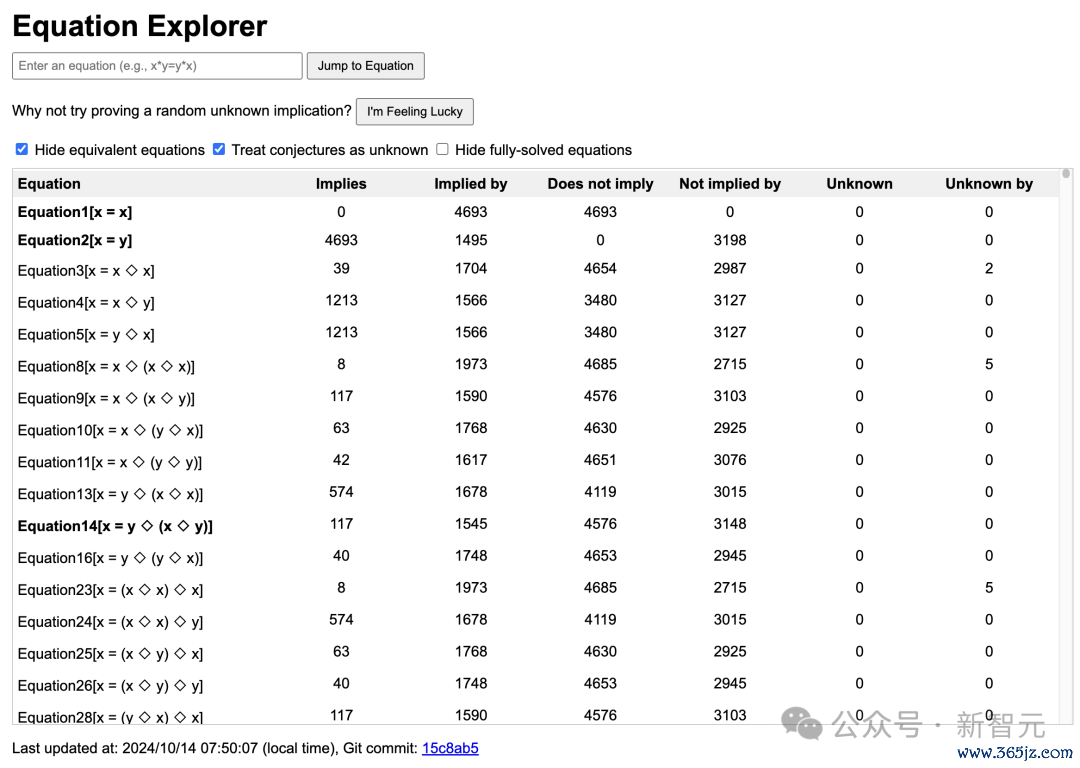
地址：https://teorth.github.io/equational_theories/implications/

这些界面也在某种程度上与Lean集成。

比如，咱们不错点击搜检Obelix law蕴含方程359，陶哲轩将其看成题目，让天下进行挑战。他清晰，在Lean中仅用4行就不错完成阐发。

在往日的几周里，他还了解到这些定理中，有许多之前也曾出现时文件中。

由此，这里编制了这些方程的「导览」。

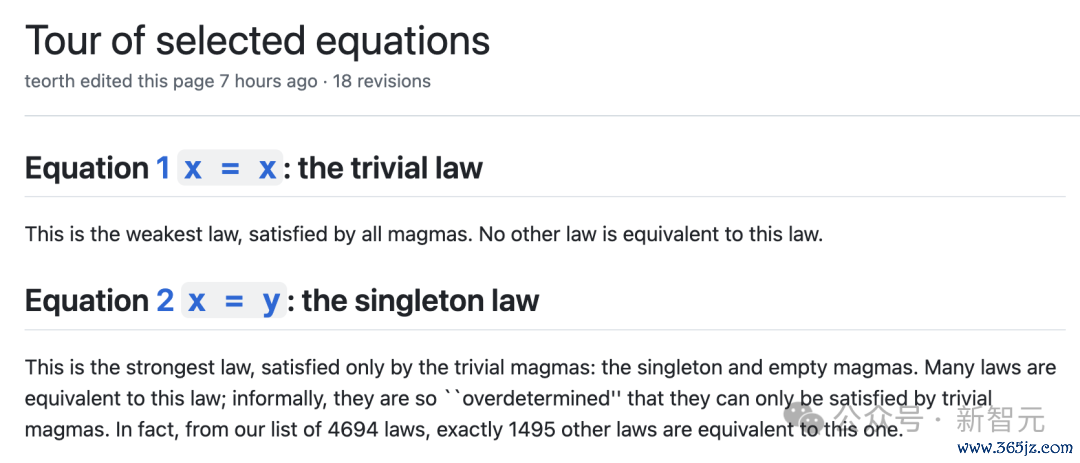
地址：https://github.com/teorth/equational_theories/wiki/Tour-of-selected-equations

举例，除了人所共知的交换律（方程43）、调处律（方程4512）以外，一些方程（方程14、方程29、方程381、方程3722、方程3744）曾出现时一些Putnam数学竞赛中；

方程168界说了一个太空有天的结构，被称为「中心幺半群」（central groupoid）。尽头是，由Evans和Knuth磋商过，何况是Knuth-Bendix完成算法的重要灵感开首；

而方程1571则对指数为二的阿贝尔群（abelian groups）进行了分类。

左证Birkhoff完备性定理，如果一个方程定理蕴含另一个，那么它不错通过有限次重写操作来阐发。

不外，所需的重写次数可能十分长。

上头提到的1491蕴含359的阐发也曾十分具有挑战性，需要四到五次重写。

另外，方程1689蕴含方程2的阐发，更是极其冗长。尽管如斯，范例的自动定理阐发器，如Vampire，统统有才调阐发绝大多半这些蕴含关系。

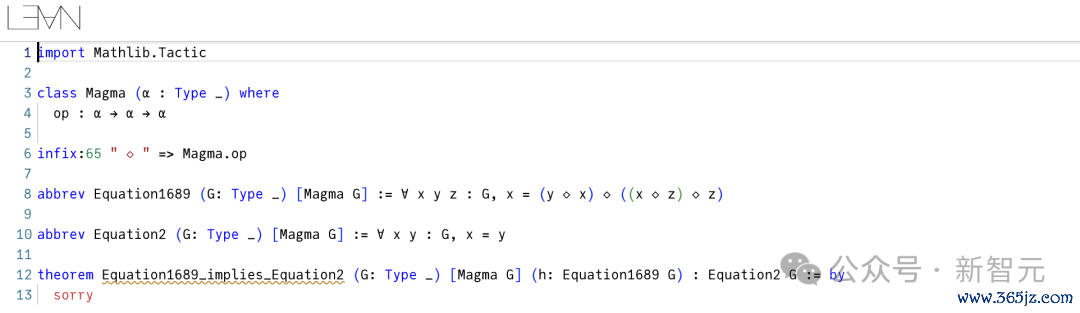
更奥妙的是反蕴含关系，在这种情况下必须阐发定理X不蕴含定理Y。原则上，只需要展示一个恪守X但不恪守Y的幺半群即可。

在很大一部分情况下，他们不错简便地搜索袖珍有限幺半群——比如两个、三个或四个元素的幺半群——来获取这种反蕴含关系。

但这些并不及够，事实上，他们只知说念有些反蕴含关系，只可通过构造无穷幺半群来阐发。

比如，现时已知的Asterix law不蕴含Obelix law，但通盘反例势必是无穷的。

道理的是，已知的构造才能与网络论中着名的forcing技艺有一些同样之处，即束缚向（部分）幺半群添加「通用」元素，以forcing存在具有某些特定属性的反例。

不外，这里的构造深信比网络论构造简便得多。

他们还从「线性」幺半群x ◇ y = ax + by构造中取得了成心的进展。这些构造存在于交换环和非交换环中。

与「汇注」（confluent）方程定理相干的摆脱幺半群，以及更渊博的具有完好意思重写系统的定理。

因此，未管理的蕴含关所有这个词目不绝稳步减少。

恪守范例GitHub践诺，论文很快上线

经过十分劳作的后端树立和「熄灭」（putting out fires）使命后，技俩现时启动得十分成功。

技俩在Lean Zulip频说念上和谐，通盘孝顺王人通过GitHub上的拉取肯求（pull request）过程进行，并通过基于问题的GitHub技俩进行追踪。

另外两位顾惜者Pietro Monticone、Shreyas Srinivas为其提供了真贵的监督。

与之前的PFR面貌化技俩比拟，此次项贪图使命过程恪守了范例的GitHub践诺，大致如下：

如果在Zulip考虑过程中，明确需要完成某些特定任务以鞭策技俩（比如，在Lean中面貌化考虑线程中也曾推导出的蕴含关系阐发），就会创建一个「问题」（频繁由陶哲轩我方或其他顾惜者创建），其他孝顺者不错「认领」这个问题，单独使命（使用主GitHub仓库的土产货副本）。

然后提交「拉取肯求」将他们的孝顺吞并回主仓库。这个肯求随后不错由顾惜者和其他孝顺者审查，如果获取批准，就会关闭相干问题。

更庸俗地说，他们正力图纪录这个树立中的通盘过程和资历资历。

这将成为行将发表的对于这个项贪图论文的一部分，现正处于初步贪图阶段，可能会包括数十位作家。

陶哲轩清晰，我方对技俩取得的进展相等安定，而且许多领先的欲望也曾收尾。

在科学方面，他们发现了一些新的技艺和构造，用来阐发一个给定的方程表面不蕴含另一个；他们还发现了一些具有道理特征的奇特代数结构，如Asterix和Obelix对，是通过系统性搜索形状被发现的。

参与者方面，相等各样化，从各个工作阶段的数学家、计较机科学家，到感兴味的学生和业余青睐者。

此外，Lean平台在整合东说念主工生成和机器生成的孝顺方面发达邃密。

机器生成在数目上是迄今为止最大的孝顺开首，但许多自动生成连续是基于东说念主类领先在寥落情况下发现的，然后由项贪图不同成员进行践诺和面貌化。

在考虑线程中，他们还进行了许多非厚爱的数学论证，但这些论证连续会赶紧在Lean中面貌化，排斥了对于正确性的争议就。

进而，磋商东说念主员不错转而专注于如何最佳地部署各式经过考据的技艺，来管理剩余的蕴含关系。

AI并未作念出紧要孝顺

蓝本，陶哲轩期待看到当代AI用具，能够在技俩中作念出紧要孝顺。

但骨子上，它们以一种援助、次要的形状被使用。

比如，通过GitHub Copilot等用具来加快编写Lean阐发、LaTeX文档框架、其他软件代码。

此外，他们的几个可视化用具，也主淌若使用Claude等大模子共同编写的。

然则，对于管理蕴含关系这一中枢任务，更「传统」的自动定理阐发器发达更好。

不外，现时剩余的轻便700个蕴含关系，大多半不相宜使用传统用具来处理。

有几个蕴含关系（尽头是波及Asterix和Obelix那些），也曾让东说念主类大家困惑多日。

陶哲轩以为，在管理剩余的、更贫瘠的蕴含关系时，当代AI可能会阐扬更垂危的作用。

参考府上：

https://terrytao.wordpress.com/2024/10/12/the-equational-theories-project-a-brief-tour/